Wave phenomena are known and studied since a very long time. Curious and complex behaviors such as dispersion, birefringence, and polarization rotation (just to name a few that occur in the optics domain) have been interpreted in terms of the underlying atomic, molecular and crystalline structure.
In the last decades people has understood that by structuring ordinary materials it is possible to obtain artificial materials whose properties go well beyond those of the constituent ones: metamaterials (from the greek meta [μετά], “beyond”). In our lab we address some questions about the physics of metamaterials and metasurfaces (i.e., the 2d equivalent of metamaterials). Our approach involves a tight cooperation between experiments performed with advanced nanostructuring techniques, numerical analysis, and analytical modeling.
Chirality
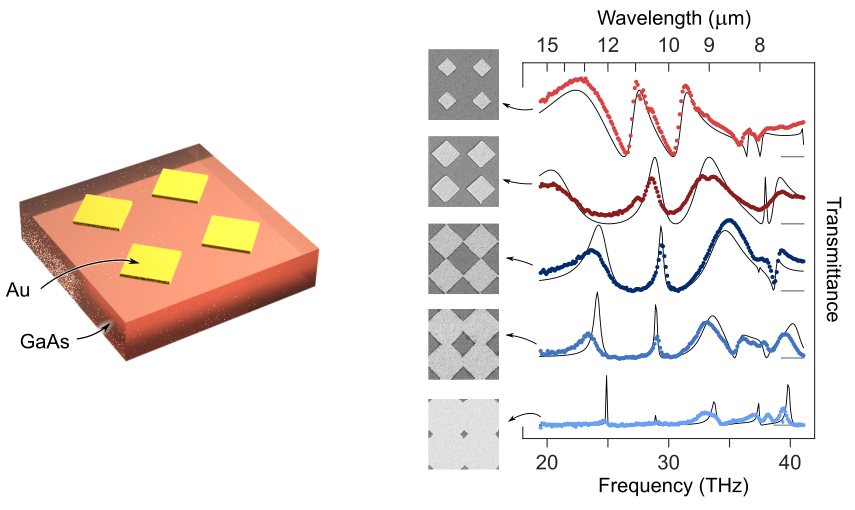
Once more from ancient Greek (kheir, χειρ) , chiral refers to something that cannot be superimposed to its mirror image. Most molecules encountered in living organisms are chiral. Also light can carry chirality; chiral light-matter interaction has a strong technological impact and scientific relevance. Patterning an achiral material with chiral inclusions leads to tailorable chiral response in the near- and far-field.

Duality and Babinet complementarity
Electromagnetic waves involve both electric and magnetic fields. There exist, however, transformations called duality transformations that exchange electric fields with magnetic ones and viceversa, giving rise to interesting mathematical properties. Curiously, those transformations allow to understand more deeper the concept of Babinet complementarity, where a screen is replaced with the complementary one. Extensions for finite-thickness and dielectric-supported screens, are, however, still reserving some surprises.
Gain and loss
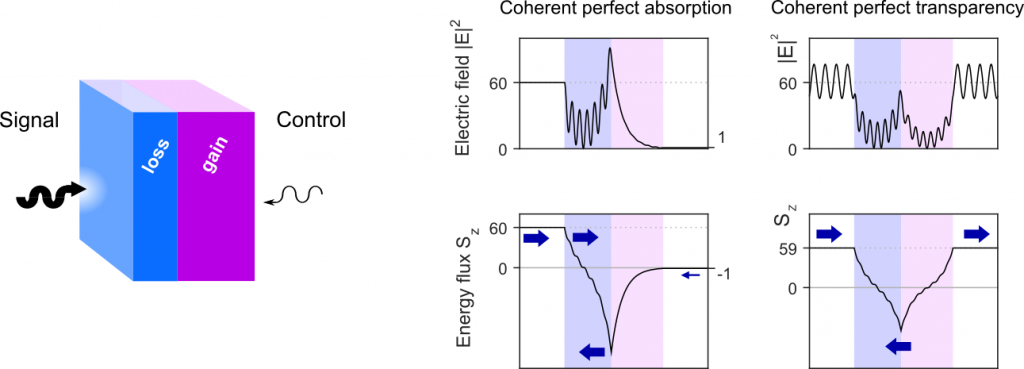
While traveling, waves can be absorbed (most of the times!) or amplified (under special circumstances like in a laser crystal). Achieving advanced control over gain and loss would allow for special operations like switching between perfect absorption and perfect transparency in the very same object. This behaviors are tightly connected with algebraic properties of the metamaterial scattering matrix such as the eigenvalues and singular values.
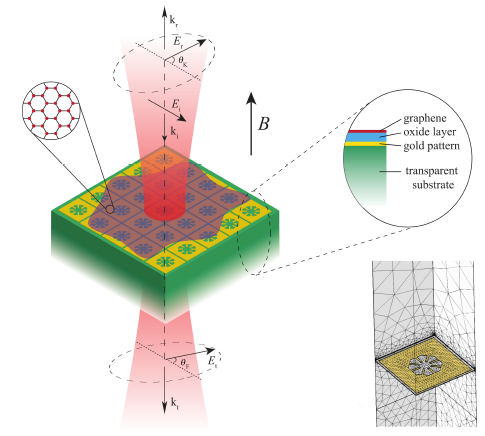
Nonreciprocity
In the most common situations of wave physics, it happens that “by interchanging source and detector the transmission remains unchanged”. This fact, which follows from profound symmetry constraints, can be violated if special materials, nonreciprocal materials, are employed. For instance, electromagnetic nonreciprocity occurs if waves are propagating in a magnetized medium. Structuration on the wavelength scale could enhance nonreciprocal effects, such as in the case of hybrid graphene-metal terahertz metasurfaces.